Skills Lab 09: The linear model (2)

Author

Today’s Session

Plotting a linear model (recap)
Fitting a linear model with one predictor (recap)
Evaluating model fit
Testing hypotheses with linear models
Creating nicely formatted output for reports (if we have time!)
Kahoot!

Tip

Kahoot quizzes are NOT assessed but are great practice for the assessed Canvas quizzes! 😉

Materials

Try out your own solutions in this document
A solutions file will be uploaded to the website after the session.

The Data

“Pet dogs (Canis lupus familiaris) release their trapped and distressed owners: Individual variation and evidence of emotional contagion”

Researchers wanted to see whether pet dogs will rescue their owners in a variety of scenarios. They collected information about each dog, including their size, age, sex, and then measured how long it took the dog to rescue their owner who was trapped in a box.

Hypothesis

Dog’s age will be a statistically significant predictor of rescue time.

Load packages and data

library(broom)
library(ggplot2)
library(rempsyc)

dog_tib <- here::here("data/dog_rescue_age.csv") |> readr::read_csv()

Codebook

dog_name - name/id of the dog
sex - dog’s sex; coded as 1 for “yes”, 0 for “no”.
rescue_time_sec - time (in seconds) it took the dog to rescue their trapped owner
vocal_distress_owner - rating of how distressed the owner sounded when calling for help, on a scale 1 (not distressed) to 6 (very distressed)
age_months - age of the dog in months
height_m - height of the dog in metres
weight_kg - height of the dog in kilograms

Task 1: Data cleaning

The age variable is currently recorded in months. For the interpretation, it might be more useful to work with years instead (will be able to tell an increase in rescue time associated with an increase of 1 year)
Create a variable called age_years that expresses the age in years instead of months.

dog_tib <- dog_tib |> 
  dplyr::mutate(
    age_years = age_months/12
  )

Task 2: Exploring the data

Before fitting any model, it helps to be familiar with your sample.

What’s the average age of the dogs in the sample?
What’s the average rescue time?
Which one of these variables is the outcome and which one is the predictor?
Create a plot showing the relationship between these two variables and interpret it. Do you think this relationship is going to be statistically significant?

dog_tib |> 
  dplyr::summarise(
    mean = mean(age_years, na.rm = TRUE), 
    sd = sd(age_years, na.rm = TRUE), 
  )

# A tibble: 1 × 2
   mean    sd
  <dbl> <dbl>
1  6.09  3.49

dog_tib |> 
  dplyr::summarise(
    mean = mean(rescue_time_sec, na.rm = TRUE), 
    sd = sd(rescue_time_sec, na.rm = TRUE), 
  )

# A tibble: 1 × 2
   mean    sd
  <dbl> <dbl>
1  22.9  27.0

Alternative if you just want to have a quick look and don’t care about whether the information is organised in tables, we could use the summary() function:

dog_tib |> 
  dplyr::select(rescue_time_sec, age_years) |> 
  summary()

 rescue_time_sec    age_years     
 Min.   :  0.73   Min.   : 1.250  
 1st Qu.:  5.16   1st Qu.: 2.417  
 Median : 12.41   Median : 6.583  
 Mean   : 22.85   Mean   : 6.088  
 3rd Qu.: 32.41   3rd Qu.: 8.333  
 Max.   :107.74   Max.   :12.000

dog_tib |> 
  ggplot2::ggplot(data = _, aes(x = age_years, y = rescue_time_sec)) + 
  geom_point(colour = "darkmagenta") + 
  stat_smooth(method = "lm", colour = "darkcyan", fill = "darkcyan", alpha = 0.2) + 
  labs(x = "Dog age (years)", y = "Rescue time (sec)") + 
  theme_light()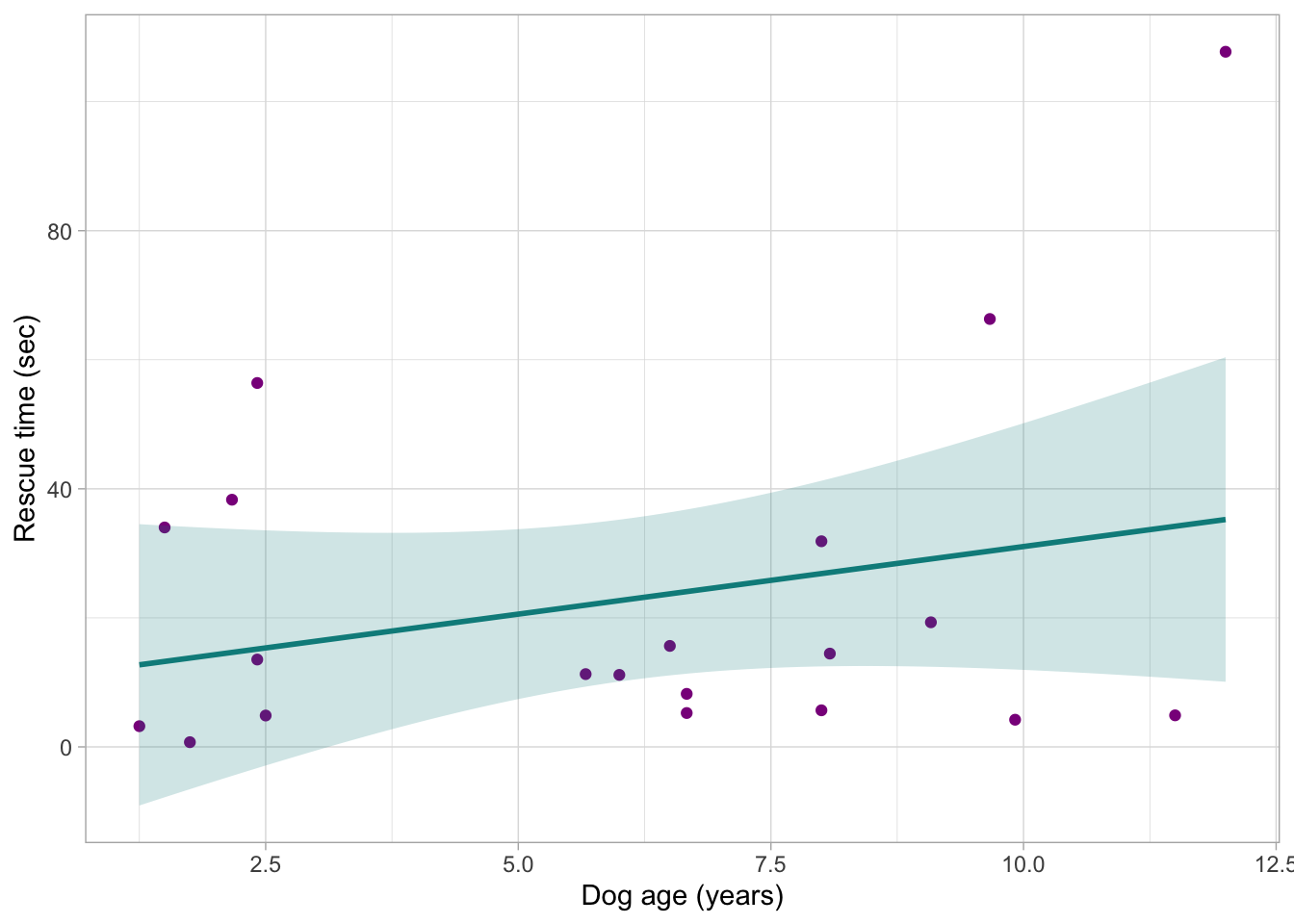

Task 3: Fitting the model

The general equation for the linear model is:

\[ y_i = b_0 + b_1x_{1i} + e \]

What is the equation for our model?

\[ \mbox{Rescue time}_i = b_0 + b_1\mbox{Dog's age}_i + e \]

Fit the model and interpret the intercept and the slope.
Use the summary() function to obtain the hypothesis test. Can we reject the null hypothesis?

dog_lm <- dog_tib |> lm(rescue_time_sec ~ age_years, data = _) 
summary(dog_lm)


Call:
lm(formula = rescue_time_sec ~ age_years, data = dog_tib)

Residuals:
    Min      1Q  Median      3Q     Max 
-29.303 -13.741 -10.150   8.948  72.500 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   10.102     12.237   0.826    0.420
age_years      2.095      1.755   1.194    0.248

Residual standard error: 26.7 on 18 degrees of freedom
Multiple R-squared:  0.07337,   Adjusted R-squared:  0.02189 
F-statistic: 1.425 on 1 and 18 DF,  p-value: 0.2481

The \(b_0\) value is 10.102, which means that when the predictor (age) is 0 years, the model predicts a rescue time of only 10.10 seconds (think back to least week about how the intercept is not always a meaningful value in the real world).
The \(b_1\) value is 2.095, rounded to 2.1. This tells us that as age increases by one unit - i.e. with each increase of 1 year - the model predicts an increase of 2 seconds in rescue time.
The p-values are listed in the Pr(>|t|) column of the output. The p-value for age_years is 0.248. This is greater than 0.05, and therefore not statistically significant. We cannot reject the null hypothesis.

Information about the model overall can be found at the bottom the output.

The multiple R² value is 0.073. This means that the model explains 7.3% of variance. This leaves 92.7% of variance in the model - or the “noise” - unexplained.

The final line tells us about the overall model fit. The non-significant p-value of 0.248 along with the low percentage of variance explained suggests that the model is, on the whole, not a good fit.

Task 4: Nicer looking summaries

When writing reports, we should never present raw R output. We can use the broom package to create nicer summaries.

Use broom::glance() to extract model fit
Use broom::tidy() to extract info about model coefficients, including confidence intervals
Pipe both outputs (individually) into the rempsyc::nice_table(broom = "lm") function to format it nicely.

dog_lm |> 
  broom::glance() |> 
  rempsyc::nice_table(broom = "lm")

r.squared	adj.r.squared	sigma	t	p	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.07	0.02	26.70	1.43	.248	1	-93.02	192.03	195.02	12,830.24	18	20

dog_lm |> 
  broom::tidy(conf.int = TRUE) |> 
  rempsyc::nice_table(broom = "lm")

Term	b	SE	t	p	95% CI
(Intercept)	10.10	12.24	0.83	.420	[-15.61, 35.81]
age_years	2.09	1.75	1.19	.248	[-1.59, 5.78]