Tutorial 05: T-test

Introduction

This week’s topic is comparing the means of two groups. We are building on the foundations of the t-distribution that we discussed in previous weeks to have a closer look at how to compare the means of two groups.

In today’s example, we’re going to be investigating the differences between two groups of people. This tutorial will walk you through the process of posing a research question, defining your hypotheses, examining and visualising the data, and finally testing and reporting the results. To do this, we will be making use of a very common statistical procedure called the t-test.

Everything you need to know in order to perform a t-test successfully will be covered in this tutorial, the Skills Lab, and the Lecture for this week.

Study Design

Today’s data comes from Mealor et al.’s (2016) paper developing the Sussex Cognitive Styles Questionnaire (SCSQ), which is a six-factor questionnaire on different aspects of how people think about and experience the world (their “cognitive style”). The paper validates the new questionnaire by comparing responses from people with and without synaesthesia.

Synaesthesia is a neuropsychological condition that usually involves automatic and lifelong associations between stimuli that aren’t usually connected. In Mealor et al.’s study, there were two different types of synaesthetes (people with synaesthesia): grapheme-colour synaesthetes and sequence-space synaesthetes.

Grapheme-colour synaesthetes experience colour when they see or think about written language, such as letters or numbers.

Sequence-space synaesthetes experience sequences - such as days of the week, months of the year, or numbers - arranged in space around them.

If you’re interested, you can learn more about synaesthesia by watching this short video by synaesthesia researcher Richard Cytowic, or by Sussex’s own Prof Jamie Ward, but it’s not necessary in order to complete the tutorial.

The SCSQ Subscales

The Sussex Cognitive Styles Questionnaire (SCSQ) has six subscales that measure different dimensions of cognitive styles. Today’s practice will focus on the Imagery Ability and Technical/Spatial subscales.

The six subscales are:

  • Imagery Ability, measuring the use of visual imagery on a day to day basis

  • Technical/Spatial, measuring spatial imagery, mathematical ability, and interest in technology

  • Language and Word Forms, measuring interest in and attention to language

  • Need for Organisation, measuring need for organisation

  • Global Bias, measuring preference for holistic vs detail-oriented thinking

  • Systemising Tendency, measuring interest in categorisation and systems

Scoring

On the SCSQ, all items are rated on a five-point Likert scale from 1 (strongly disagree) to 5 (strongly agree).

For each subscale, a person’s score is calculated as the mean rating on the items belonging to that scale. A higher score indicates a greater preference for the cognitive style that the subscale represents.

Right, enough background! Let’s dive in.

Task 1

Load the necessary packages and data.

  1. Load the tidyverse package. We’ll also be using the new ggrain package, so you can load that one as well.
  2. Read in the data saved in syn_data.csv, which is in the data folder.

You’ll need to use the library() function to load packages. This function needs to be called somewhere at the beginning of the document.


Next


You can read datasets with readr::read_csv().


Next


The dataset is in the data folder. Have a look at previous tutorial examples if you don’t remember how to specify a file path.


# read in the data 
syn_data <- here::here("data/syn_data.csv") |> readr::read_csv()

Codebook

Variable Name Variable Type Description Notes
id_code Categorical Participant ID code
gender Categorical Gender identity Numeric codes represent the following identities:
0 = Female
1 = Male
gc_score Numeric Score on the grapheme-colour diagnostic test (Eagleman et al., 2007)
syn_graph_col Categorical Self-report of grapheme-colour synaesthesia
syn_seq_space Categorical Self-report of sequence-space synaesthesia
syn Categorical Whether the participant has any kind of synaesthesia or not Either 'Synaesthete' (reports any or multiple types of synaesthesia) or 'Non-Synaesthete'
scsq_imagery Numeric Score on the SCSQ Imagery subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
scsq_techspace Numeric Score on the SCSQ Technical-Spatial subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
scsq_language Numeric Score on the SCSQ Language subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
scsq_organise Numeric Score on the SCSQ Organisation subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
scsq_global Numeric Score on the SCSQ Global subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
scsq_system Numeric Score on the SCSQ Systematising subscale Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style
overall_img Numeric Mean of SCSQ Imagery and Technical-Spatial subscale scores Mean score on scale from 1 to 5. Higher scores indicate greater tendency towards that cognitive style

Data Preparation

Task 2

Inspect your dataset, and compare it to the Codebook. Identify any discrepancies between the two, using the Codebook as a guide for what your dataset should look like and what variables it should contain.

Make a list below of the steps you must take to clean or change your dataset so that it matches the Codebook, then do them.

Obtain some basic summaries of your dataset. Compare each variable to its description in the Codebook one at a time. Ask yourself:

  • Does this variable also appear in the dataset, or does it need to be created/changed?
  • Is this variable the right type of data?
  • Does it contain the values or ranges of values it should contain?

Next


For variables that need to be created, should the new value be calculated the same way for everyone, or should different cases receive different values depending on particular conditions? If so, what condition(s) are there?


Obtain some basic summaries with e.g. summary():

summary(syn_data)
    id_code           gender          gc_score      syn_graph_col     
 Min.   :   1.0   Min.   :0.0000   Min.   :0.3500   Length:1211       
 1st Qu.: 303.5   1st Qu.:0.0000   1st Qu.:0.5600   Class :character  
 Median : 606.0   Median :0.0000   Median :0.7200   Mode  :character  
 Mean   : 606.0   Mean   :0.1982   Mean   :0.7558                     
 3rd Qu.: 908.5   3rd Qu.:0.0000   3rd Qu.:0.8750                     
 Max.   :1211.0   Max.   :1.0000   Max.   :1.4000                     
                                   NA's   :1168                       
 syn_seq_space       scsq_imagery   scsq_techspace scsq_language  
 Length:1211        Min.   :1.240   Min.   :1.24   Min.   :1.000  
 Class :character   1st Qu.:3.410   1st Qu.:2.41   1st Qu.:3.000  
 Mode  :character   Median :3.760   Median :2.82   Median :3.670  
                    Mean   :3.715   Mean   :2.86   Mean   :3.581  
                    3rd Qu.:4.060   3rd Qu.:3.29   3rd Qu.:4.170  
                    Max.   :5.000   Max.   :4.88   Max.   :5.000  
                                                                  
 scsq_organise    scsq_global     scsq_system   
 Min.   :1.000   Min.   :1.000   Min.   :1.000  
 1st Qu.:2.670   1st Qu.:2.500   1st Qu.:2.170  
 Median :3.170   Median :2.880   Median :2.670  
 Mean   :3.109   Mean   :2.939   Mean   :2.672  
 3rd Qu.:3.670   3rd Qu.:3.380   3rd Qu.:3.170  
 Max.   :5.000   Max.   :5.000   Max.   :4.830

The variables syn and overall_img do not exist in the dataset (yet). Optionally, but preferably, the gender variable should be recoded.

For the syn variable, different cases should receive different values, so we need case_when(). The quickest way to define a condition like this is to actually slightly reverse it. If some isn’t a grapheme-colour synaesthete AND if this person also isn’t a sequence-space synaesthete, they get the value “Non-Synaesthete”. In all other cases they get “Synaesthete”. (If this isn’t how you solved this bit, that’s fine - as long as you came up with the same output!)

For the overall_img variable, the new variable is the mean of two other variables, which we’ve already seen previously. For the gender variable, this requires relabeling as we have also seen previously.

All three of these changes can be done in a single mutate() command, each as its own argument.

syn_data <- syn_data |> 
  dplyr::mutate(
    syn = dplyr::case_when(
      syn_graph_col == "No" & syn_seq_space == "No" ~ "Non-Synaesthete",
      .default = "Synaesthete"
    ), 
    overall_img = (scsq_imagery + scsq_techspace) / 2,
    gender = dplyr::case_when(
      gender == 0 ~ "Female",
      gender == 1 ~ "Male",
      .default = NA
    )
  )

Research Question

Today we will be walking through the process of conducting an independent samples t-test. This test compares the means of two groups (“samples”) which each contain different entities/people (“independent”). We will test the null hypothesis that the sample means from our two independent groups are drawn from the same population.

To translate that into our current dataset, we will be comparing the means of overall imagery scores between groups of people with synaesthesia and people without. The difference in imagery between synaesthetes and non-synaesthetes is well-documented; see e.g., O’Dowd et al. (2019). These groups are also independent by definition: a person can either have synaesthesia or not, but they can’t be in both groups at once.

Stop and think about this before we go on. If you need a refresher, look back on the Lecture on Null Hypothesis Significance Testing (Week 4) for a reminder of how to define the null and alternative hypotheses.

Task 3

Using the lectures from Weeks 04 and 05, answer the following questions in your Quarto document.

  1. What is the alternative hypothesis for this study? What pattern would we expect to see in the data if the alternative hypothesis were true?

  2. What is the null hypothesis for this particular study? What pattern would we expect to see in the data if the null hypothesis were true?

  3. Make a prediction: What do you think we will find? Do you think that there will be a difference in overall imagery ability?

  4. What alpha level would you choose for this test?

Important

Don’t just look at the solution! Take a moment to think it through and write down your thoughts in your Quarto document before you move on.

  1. The alternative hypothesis is that synaesthetes and non-synaesthetes differ in overall imagery ability. In other words, being a synaesthete or not has a relationship with overall imagery ability. If the alternative hypothesis is true, we would expect to see a significant difference in the overall_img for these two groups.

  2. The null hypothesis is that synaesthetes and non-synaesthetes do not differ in overall imagery ability. In other words, being a synaesthete or not has no relationship to overall imagery ability. If this is the case, taking samples of imagery scores from synaesthetes and non-synaesthetes is the same as sampling from a single population of imagery scores. If the null hypothesis is true, we would expect to see no difference in the overall_img for these two groups.

  3. This question is asking you about your opinion - what do you think?

  4. Again, if you have enough information about the context, you can choose any sensible alpha level. For now, it’s fine to stick with .05.

Now that we have our hypotheses and prediction nailed down, let’s visualise the data.

Visualisation

Let’s visualise the differences between group means to help us understand our data better. We’ll start with a basic plot and build it up from there to create a publication-worthy, report (or take-away-paper!) -quality plot. We’ll also suggest some optional extras to make your plots extra fancy, but you’ll have to do the legwork!

We’re going to try out a new type of plot today: the raincloud plot. Raincloud plots are named because they include a density plot (basically a smoothed histogram) with a scatter of the data points underneath, which kind of look like clouds with raindrops. They contain a ton of useful information all at once: the distribution of the data, the actual data, and often some summaries of the data (such as boxplots or means). Although they’re a bit more complex to read and interpret, they’re more efficient uses of space and allow quick comparison of multiple important measures.

Revision of {ggplot2}

Revision Ahead

This section contains revision of constructing data visualisations with the {ggplot2} package. It’s been a while since PAAS, so this section is included to help you refresh your memory.

The {ggplot} package is a bit of a universe in its own right. The “gg” stands for “grammar of graphics” - in other words, a language (“grammar”) for creating visualisations (“graphics”). We’ll see more examples each week of different kinds of plots you can build, and you may have already created some previously in PAAS.

Layers

Plots in {ggplot2} are built in layers. Each layer adds to or changes something about the plot; these can be big elements, like determining the type of plot to create, to small details like editing axis labels or changing colours. In {ggplot2}, each layer is a function.

If it helps, you can think of layers like different colours in a linocut print. Each additional layer of colour adds a bit more to the overall picture, building up from big blocks of colour to small details.

To build a visualisation in {ggplot2}, it’s a good idea to build your plot in the same way, from big picture to small detail. As we’ll see, we recommend building plot layers like this:

dataset |> 
  aesthetics_mapping +
  choose_type_of_plot +
  add_more_elements +
  edit_labels_or_colours +
  apply_a_theme

These are guidelines, but the general => specific flow is for a good reason: layers are evaluated from top to bottom. So, it’s best to get the big pieces in place first, then fine-tune, than to have those fiddly bits overwritten by a major change at the end of the code.

Notice as well that layers are added to a plot object with + and NOT with |>. This is specific to {ggplot2} (AFAIK!) and is easy to forget, but don’t worry - it’s such a common thing that {ggplot2} has a very friendly error message for fixing it.

The actual error that pops up when you use a pipe instead of + isn’t super transparent. However, there is a very friendly reminder directly underneath to nudge you in the right direction. It’s a good reason to always read the error message in full!

syn_data |> 
  ggplot(aes(x = scsq_imagery)) |> 
  geom_histogram()
Error in `geom_histogram()`:
! `mapping` must be created by `aes()`.
ℹ Did you use `%>%` or `|>` instead of `+`?

Mapping

As we saw in the error just above, mapping is created with aes(). This little function defines the aesthetics of the plot - in other words, this is how you tell R what data you want it to plot. We’ll use the following general format to set up a plot:

dataset_name |> 
  ggplot(aes(x = variable_on_x_axis, y = variable_on_y_axis, ...))

The ... takes additional arguments to add things like colour and fill.

Geoms, etc.

So, how do we actually add layers? There are several common types of functions with shared prefixes that do particular things. We’ll meet lots of examples of them just below, but as a quick reference for some of the more common function types.

Note that in the names below, the * is a wildcard placeholder. This means that, for example, geom_*() stands in for a family of functions where the * could be many different things: geom_point(), geom_bar(), geom_histogram(), etc.

  • geom_*(): Draw geometric objects to represent the data.
  • stat_*(): Add elements to the plot calculated with statistical functions.
  • scale_*(), labs(), and lims(): Adjust the appearance of the axes (labels, title, limits, etc.) or quickly adjust the labels or limits only
  • guide_*(): Make adjustments to the scales or to other interpretational elements of the plot (such as legends for categories)
  • theme_*(): Apply a pre-made theme to the entire plot
Tip

See the {ggplot} reference documentation for a comprehensive list and detailed guide to these functions and more.

Right, the best way to get a handle on these functions is to start building plots! So let’s jump in.

Task 4

Build a raincloud plot with group means and confidence intervals using the following steps.

  1. Create a base ggplot layer with synaesthete status on the x-axis and overall imagery ability on the y-axis.
  2. Use the geom_rain() function to create the raincloud plot.
  3. For a t-test, we’re primarily interested in the group means, but we don’t have them represented by default in the raincloud plot. Add in a layer with the means and CIs, as we did in the Skills Lab. To make sure we can see the means on top of the scatter of points, you should also add a colour = argument.
  4. Format and theme your plot by adding axis labels, setting the limits on the y-axis to 1 and 5, and adding a theme.

Look through the hints below if you don’t remember how to do these steps!

As a reminder, the general form of a ggplot is:

dataset |> 
  ggplot2::ggplot(aes(x = variable_for_the_x_axis, y = variable_for_the_y_axis)) + 
  some_plotting_function()

The first line is the base layer referred to in point (1). The second line can be replaced with geom_rain() as instructed in point (2).

At this point, you should already have a basic plot! Run your code to see what you have so far.


Next


The function to add means and CIs to your plot is stat_summary(fun.data = ????), where the ???? is the name of the same function that we used to calculate CIs for our summary tables in the previous tutorial.

Don’t forget to add the colour = argument, and pick any colour name or hex code you like.


Next


You can use the labs() shortcut to adjust axis labels easily, but personally I prefer to go the long way round and use the scale_*() family instead. These functions have specific names depending on which axis scale you want to adjust, and the way that data is measured. In this case we want to adjust the y-axis and the data is continuous, so the function we need is scale_y_continuous().

The advantage of going through the extra trouble to use the scale_*() functions is that they allow you to adjust everything about that scale at once. So, we can use the arguments for scale_y_continuous() to change the axis label with name =, the breaks with breaks =, the limits with limits = …well, I’m sure you get the idea!

To change the x axis, we only really need to change the axis label, so the labs() function is fine here.


Next


The last step is to choose a theme. There are a good few that come installed with {ggplot2}, and they all start with theme_. Try out a few and see which one you like best.


Here’s how we can create a raincloud plot. I chose theme_bw() because it’s clean and simple, but if you chose something else, that’s fine.

1syn_data |>
2  ggplot(aes(x = syn, y = overall_img)) +
3  geom_rain() +
4  stat_summary(fun.data = mean_cl_normal,
               ## Any colour you like is fine!
               colour = "darkcyan") +
5  scale_y_continuous(name = "Mean Overall Imagery",
                     limits = c(1, 5)) +
6  labs(x = "Presence of Synaesthesia") +
7  theme_bw()
1
Take the dataset, and then…
2
Create a plot with synaesthesia status on the x-axis and overall imagery score on the y-axis
3
Draw a raincloud plot
4
Add means and 95% CIs, in dark cyan
5
Adjust the continuous y axis to change the name, and to set the limits to 0 and 5
6
Change the label of the x axis
7
Add a black-and-white theme

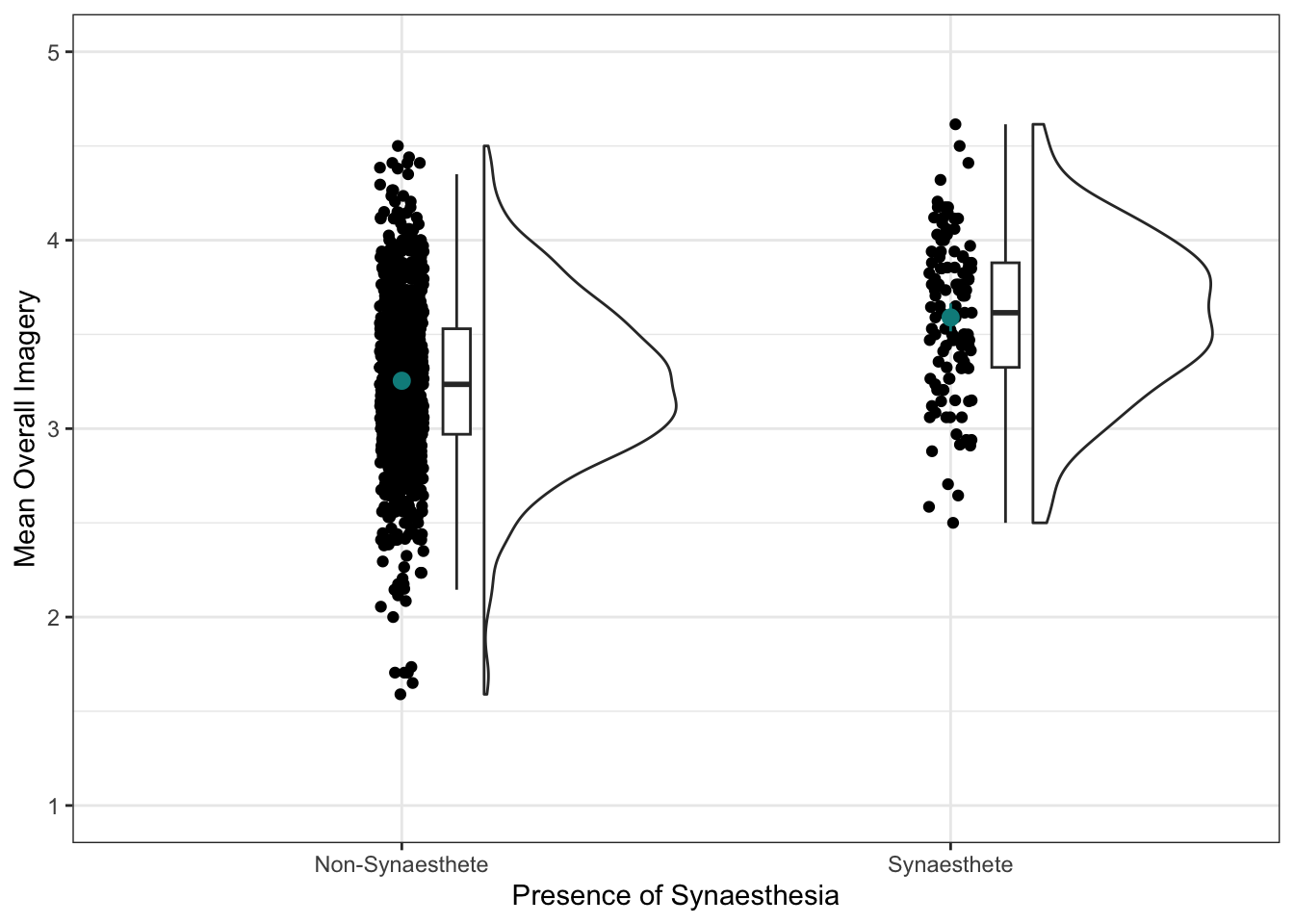
Nicely done! This plot is great, and would work well for a take-away paper, for example. If you’re keen to move on, you can skip the optional section below, but if you’d like to make your raincloud plots even nicer, give it a try.

Want a bit more out of your plots? Here are some suggestions you can look into to make your plot unique. Remember, if you get stuck and can’t get them to work, ask us in a practical or drop-in!

Add Colour by Group

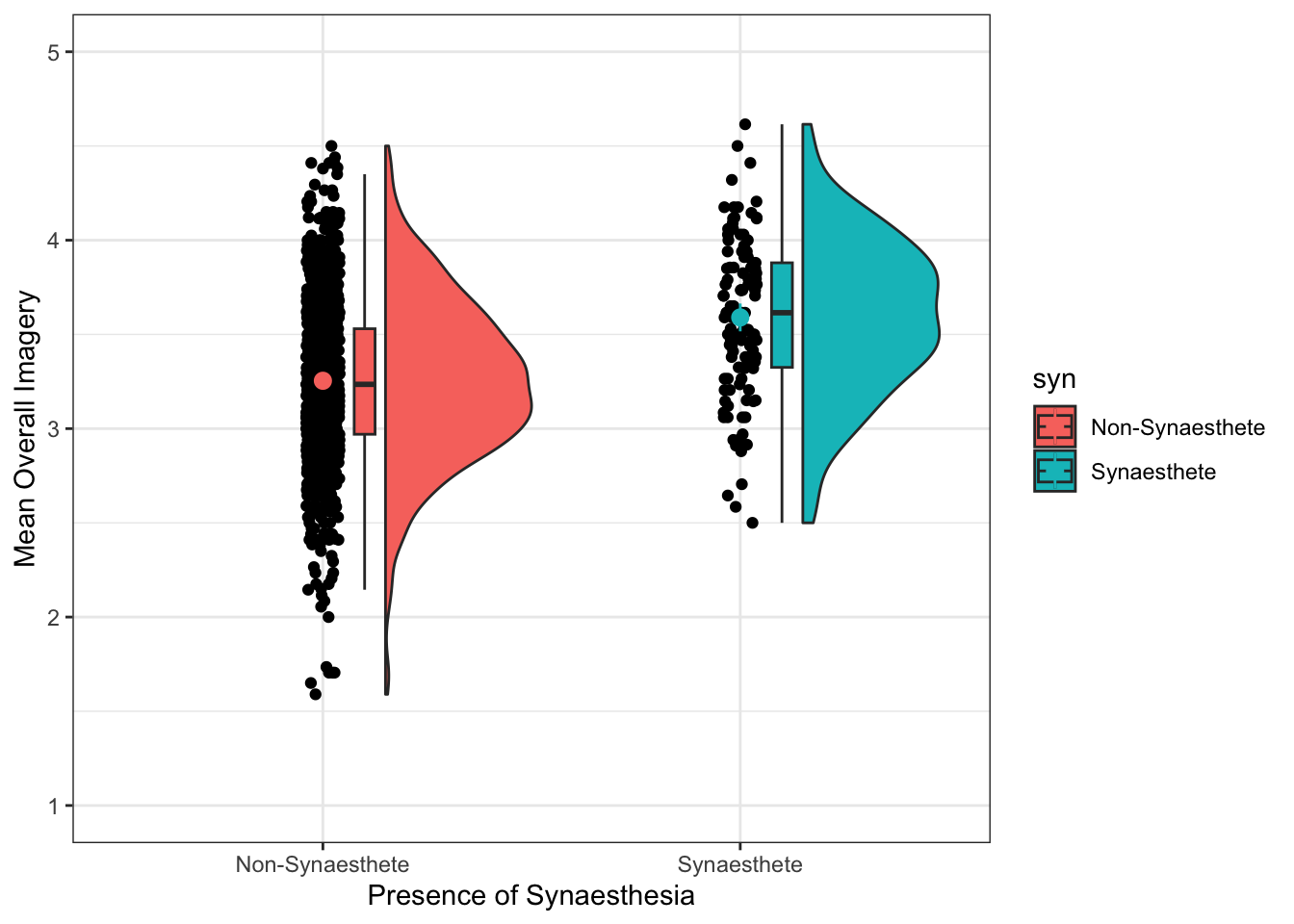
Check out the fill = and colour = arguments for aes() in the very first line of ggplot(). See if you can recreate this plot:

Transparency, Shape, and Colour

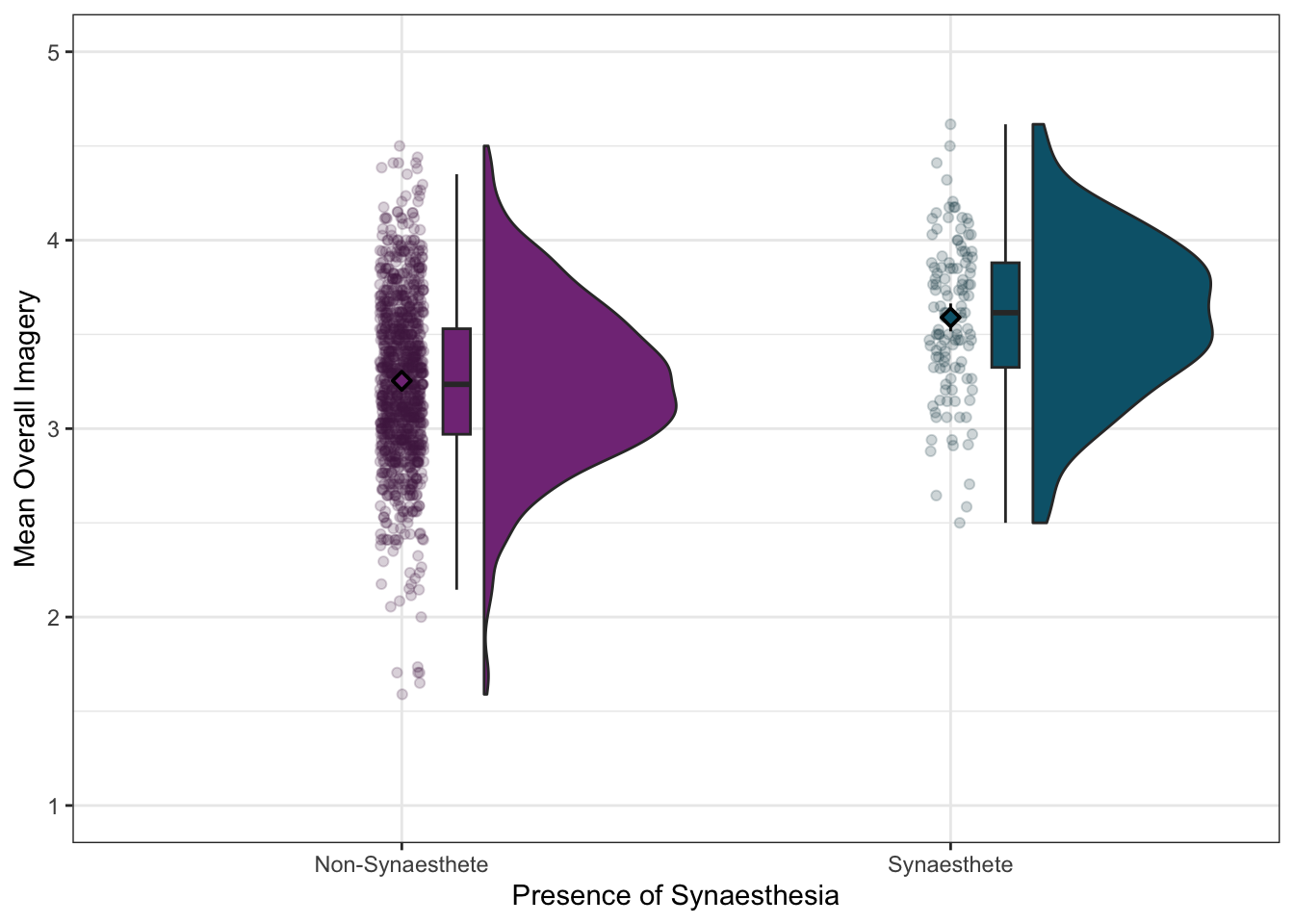
Those solid black dots and garish default colours are awful! Check out the alpha = and shape = arguments to adjust the transparency of the dots and the shape of the means. Then, try applying some colours and getting rid of the superfluous legend on the right-hand side.

Some packages come with “vignettes”, which are essentially tutorials about how a particular package works. They’re a massive help especially if you are stuck on a complicated task.

Lucky for us, there’s a lovely and very helpful vignette for raincloud plots! To open it, run vignette("ggrain") in the Console and have a look through.


Next


This is tricky and involves changing several things about the plot. Compare the plot you are trying to make to the one you have and try to identify what is different. Then, identify which layer does creates those elements - or if you need a new layer altogether!


Task 5

Interpret the plot and write down your thoughts in your Quarto doc. What can you learn from this visualisation of the data?

Some things you could look at include: which group mean (the dot) is higher? How large is the difference? Do the confidence intervals overlap? Is the spread of the scores roughly equal for the two groups or are they different?

Sorry, no answers here. If you’re not sure what you should get from this plot, review the Skills Lab, or ask us in a practical or drop-in.

Now that we’ve had a look at our data, we can move on to actual statistical testing!

The t-test

So, we’ve made our predictions, and we’ve had a look at the data. Now we’re ready to conduct our t-test.

In order to find out whether people with and without synaesthesia differ in their imagery ability, the test follows this process:

  1. We’ll need the mean overall imagery in each group. These two means represent our best guess about overall imagery ability for people who have have synaesthesia and who don’t.

  2. Next, we’ll calculate the difference in the means between the two groups. This difference is a measure of the effect - the size of the impact on overall imagery associated with being a synaesthete or not.

  3. Then, we will calculate an estimate of the standard error of the difference in the means. This is a measure of the error - how much variation there is among the differences in the means.

To calculate our test statistic, t, we then simply compare how big the effect is compared to the error. You can think of this as a signal-to-noise ratio - how big is the “signal” (the difference in imagery associated with synaesthesia) against the background of the “noise” (the variation in estimates of that difference in imagery)? In other words:

\[ t = \frac{\text{difference in means}}{\text{estimated standard error of the difference}} \]

From here, we’re in familiar territory. We have a test statistic, t, that we will calculate for our data. Since we’ve already practiced working with distributions, probabilities, and critical values, we know that all we need is the t-distribution with the right degrees of freedom. With that information, we can find the probability, p, of obtaining the t-value that we calculated, or a more extreme one, assuming the null hypothesis is true.

The good news is, all of the calculations and values we need will be calculated by R for us, as we will see as we progress. Doing the calculation is R’s bit; interpreting the results and understanding what they mean for our understanding of the world is ours!

Task 6

Complete the following steps:

  1. Write a formula that represents the relationship between our variables. This has the general form outcome_variable ~ grouping_variable. What would this be for our study comparing overall imagery score between synaesthetes and non-synaesthetes?
  2. Use the t.test() function to perform an independent samples t-test on the syn_data data to find out whether there is a difference in overall_img between syn groups. To to do this, you need to use the formula you wrote in the previous step, and you’ll also need to tell the t.test() function the name of the dataset where it can find the variables.
  3. The last argument in the t.test() function should be alternative = "two.sided". This tells R to run a two-tailed test, instead of a one-tailed test.
  4. Save the result into an object called syn_t.

If you need help with the t.test() function, you can always open the help documentation using ? or help().


Next


The outcome variable here is overall_img and the grouping variable is syn. Therefore, the formula can be written as…


Next


…

overall_img ~ syn

The next step is to put this inside of the t.test() function and specify the dataset.


Next


Don’t forget the alternative = "two.sided" argument as instructed.


Use the t.test() function to perform the t-test:

syn_t <- t.test(overall_img ~ syn,
         data = syn_data,
         alternative = "two.sided")
syn_t

    Welch Two Sample t-test

data:  overall_img by syn
t = -8.5053, df = 150.58, p-value = 1.67e-14
alternative hypothesis: true difference in means between group Non-Synaesthete and group Synaesthete is not equal to 0
95 percent confidence interval:
 -0.4141795 -0.2580225
sample estimates:
mean in group Non-Synaesthete     mean in group Synaesthete 
                     3.253940                      3.590041

Interpretation

Let’s interpret the results, now that we finally have them. For statistical results, when we say “interpret” results, what we mean is to translate the statistical output, like we got from the t.test(), back into the context of our original research question. The questions in the task below will help walk you through this process.

Task 7

Write down the answers to each question about interpreting the t-test results in your Quarto doc:

  1. How big is the difference between the means?

  2. Is a t of -8.51 a big difference? How do you know?

  3. What is the probability of obtaining this value of t under the null hypothesis?

  4. Putting everything together, what can we learn from this result? Write down what you understand from this test in your own words.

The mean difference isn’t actually in the output - you’ll need to calculate it by subtracting mean in group Synaesthete from mean in group Non-Synaesthete.

  1. The mean difference was -0.34 (3.2539404 - 3.5900413 rounded to two decimal points.)

  2. It’s not possible to tell whether a t of -8.51 is large or small. The value itself is large enough to result in statistical significance but the t statistic depends on the sample size. So with large sample sizes, even tiny differences result in a large t. It’s more helpful to look at the mean difference.

  3. We want to look for the p-value here, which is 1.6704292^{-14}. This is scientific notation - the “e-14” means that we should shift the decimal point of the preceding number 14 places to the left, resulting in a value 0.000000000000016704292. So, this is a very tiny number! In cases like this, we can just write p < .001. So the probability of obtaining t at least as large as -8.51 is less than 0.001 (which is equivalent to 0.1%).

  4. We know that the difference between the scores of synaesthetes and non-synaesthetes was statistically significant - therefore we can reject the null hypothesis. The difference itself, however, was quite small - only -0.34. The confidence interval for this difference tells us that the difference in the population could be as small as -0.26 or as large as -0.41, assuming that our sample is one of the 95% producing confidence intervals containing the population value (i.e. even at the extreme ends, the difference is small).

Reporting

Each well-known statistical test has a specific format for reporting the numerical results in formal situations, such as a report or journal article. Here’s the basic format for t-tests in APA style:

estimate_name(degrees_of_freedom) = estimate_value, p = exact_p, Mdiff = difference_in_means, 95% CI = [CI_lower, CI_upper]

In APA style, we’ll round all numbers to two decimal places where appropriate, except for p. We round p to three decimal places, unless it’s smaller than .001, in which case we simply report “p < .001”.

What’s MDiff?

Everything we’ve reported above we’ve seen before, except for Mdiff. This represents the differences in the means of the two groups. This is a key element of the t-test, but it’s also important because the 95% CIs are an interval estimate around that mean difference. Without reporting Mdiff, the CIs are quite hard to interpret!

As a side note, you can subscript letters in Quarto by surrounding them before and after with ~s like this: *M*~diff~

Task 8

  1. Use the APA format and the values from your output to type out the result of the t-test.
  2. Put all of this together into one report of your findings, both in plain language and including all of the relevant statistical results, such as the M and SD in both groups and the results of your statistical test. See the lecture for an example.

You’ll need to use the values from the previous task to complete this exercise. You might also want to compute some grouped summaries for mean and SD of each group.

You could write something along the lines of:

On average, synaesthetes (M = 3.59, SD = 0.41) scored higher on overall imagery than non-synaesthetes (M = 3.25, SD = 0.43). The difference between mean imagery scores was statistically significant, t(1211) = -8.51, p < .001, Mdiff = -0.34, 95% CI [-0.41, -0.26].

Together with the graph we already made, this is a thorough and well-reported analysis!

Recap

Well done conducting your t-test.

In sum, we’ve covered:

  • How to create professional plots representing the key relationship of interest

  • How to run the independent samples t-test and read the output

  • How to report and interpret the statistical results of these tests in real-world terms

Remember, if you get stuck or you have questions, post them on Discord, or bring them to practicals or to drop-ins.

If you’re feeling warmed up now, take on the ChallengR below to test out your new analysis skills.

ChallengR

ChallengR Time!

This task is a ChallengR, which are always optional, and will never be assessed - they’re only there to inspire you to try new things! If you solve this task successfully, you can earn a bonus 2500 Kahoot Points. You can use those points to earn bragging rights and, more importantly, shiny stickers. (See the Games and Awards page on Canvas.)

There are no solutions in this document for this ChallengR task. If you get stuck, ask us for help in your practicals or at the Help Desk, and we’ll be happy to point you in the right direction.

The main part of this tutorial is an independent measures t-test, when the two groups being compared contain different (“independent”) people or entities. However, in the lecture we also covered a second type: the repeated-measures t-test, when the two groups being compared contain the same people or entities in different conditions, at different timepoints, etc. For this task, you will need to prepare for, run, and report a repeated-measures t-test.

Data and Design

The dataset for this task is an expanded version of the same kind of design described in the lecture about training synaesthesia, but this time for colours for musical notes. In this hypothetical study, participants were first tested on a Stroop-style task, where they were presented with a pure tone musical note and a block of colour on a screen, and were asked to respond to the colour as quickly as possible. Then, over the course of several weeks, participants underwent training where they heard different tones paired with different colour lights. Finally, the participants again completed the same Stroop-style task as the beginning. The researchers hypothesized that this training would lead to significantly quicker response times after training compared to before, indicating an automatic connection between music and colour.

The dataset contains the following variables:

  • id: ID code of the participant
  • time: Coding variable of the timepoint, either “pre” or “post” the training
  • response_ms: Response latency to tap the target colour, in milliseconds

Task 9

  1. Read in the data saved in syn_train.csv, which is in the data folder, and have a look at it
  2. Generate a summary table presenting relevant descriptive statistics for this design. You can format it nicely if you like for practice.
  3. Perform the appropriate t-test and make sure you understand what the results mean.

Overall descriptives of response latency won’t be very helpful here. Make sure to split up your descriptive output by timepoint.


Next


You will need a new argument for the t.test() function that we haven’t explicitly practiced yet. This new argument should express what kind of test you want to perform - whether the data are repeated, or paired, or not. You will get a very different answer depending on what type of test you do! To find out what this argument is, use the help documentation for the t.test() function.


Once you have your output, take the Week 5 ChallengR quiz on Canvas and use the output to answer the questions. Good luck, and well done again!