Tutorial 09: Linear model (2)

Introduction

Last time you learnt about the equation for a straight line and how it can be used to model a relationship between a predictor and an outcome variable by fitting a linear model to data. In this tutorial, we’ll talk about how we find line of best fit that characterises the linear model and also what we mean by “best fit”. In other words, we’ll see how we can find the values of the intercept and slope of the line that fits the data best. We will also talk about how the linear model is tested in the framework of Null Hypothesis Significance Testing (NHST). Finally, once we’ve found and tested our linear model, we will see how we can evaluate how good this model is.

Warm-up Quiz

Before we start, why not get in the mood by answering a few quiz questions!

Remember, the equation for the linear model is

\[y_i =b_0+b_1x_i+e_i\]

Or if writing out the multiplication sign makes it clearer, we write:

\[y_i =b_0+b_1\times x_i+e_i\]

Question 1

What does b₁ represent in the formula?

The intercept of the outcome variable for a given slope The predictor variable in the model The value of the outcome when the predictor is equal to zero The increase in outcome per unit increase in predictor

Question 2

What value of the outcome does the model y_i = 13 − 2.5 × x_i predict when the value of the predictor is 4? (give answer to 2 decimal places)

Question 3

What outcome value does the same model predict when the the predictor is −1? (give answer to 2 decimal places)

Question 4

What kind of relationship is this?

Neutral Negative Positive None

What about the little i guy?

The \(i\) subscript in \(y_i\)¹, \(x_i\), and \(e_i\) is the index of the given data point. You can imagine it as the row number in your data set: \(i = 1\) is the first row, \(i = 2\) is the second row, \(i = n\) is the \(n^{\text{th}}\) row of your data.

Let’s say that we’re working with human participants. Participant 1 will get their score on the variable \(x\). We label their score as \(x_1\) . The score of participant 2 will get the label \(x_2\), and so on. Likewise, the model will predict different values of \(y\) depending on what the value of \(x\) is. For participant 1, the model will predict some value of \(y_1\), for participant 2, this will be \(y_2\) . For each participant, there will also be an error (or difference) between what the model predicts, and what the actual values of \(y\) is. Participant 1 gets error \(e_1\), participant 2 gets \(e_2\).

Writing this out for all participants in the model would get very tedious very quickly. So we replace the number with \(i\) , to represent any participant from the sample (more general term for a “participant” can be a “case”, which is a term often use).

However, the model intercept and slope (the \(b_0\) and \(b_1\) coefficients) are the same for every point, and so they do not have an \(i\) subscript.

Setting Up

In this tutorial, we’ll return to the same model we fit last week. That way, we can compare what we learned using the actual values in the model to how we can evaluate those values.

Task 1

Load packages and data

We’ll be using a new package today called broom along with good old tidyverse .

Load the necessary packages.
Read in the gensex.csv dataset using the code chunk below.
Explore the dataset to remind yourself of the variables it contains.

# read data 
gensex <- here::here("data/gensex.csv") |>
  readr::read_csv()

Hint

You need to use the library() function to load each package.

You can add this into a code chunk somewhere at the top of your tutorial notebook”

library(broom)
library(tidyverse)

What is “best fit”?

In the lectures, we’ve talked briefly about a “line of best fit”, but what does “best fit” actually mean? Take a moment to play with the intercept and slope of the line in the plot below. Use the yellow circles to drag the line to a position where you think it adequately fits the scattered data points.

If you’re thinking that it’s not really obvious how precisely to fit the line, you are correct! It’s really difficult to just eyeball the position and orientation. What we need is some sort of criterion for deciding which line fits the data best.

Deviations and Residuals

Deviation is the difference from each point in the data from some place, for example the mean. We use deviations to quantify the amount of variability in a variable. You may recall that standard deviation is the average distance of each point from the mean in a sample. However, because the individual distances of each point from the mean of a variable always add up to zero, we calculate the squared deviations and add those up. The result of this operation is the sum of squares and it is the basis for the calculation of the variance and the standard deviation.

Just like we can calculate the distance of points from a mean (another point), we can calculate their distance from a line. Let’s see what that looks like.

In the applet above, change the slope and intercept of the line so that it is the same as the dashed line that represents the mean of the y variable (the line needs to align with the horizontal dashed line) Then, answer the questions.

Question 5

What is the intercept of this line?

0 Constant for all values of y Mean of x Mean of y

Question 6

What is the slope of this line? (2 decimal places)

The thin dashed lines connecting each point with the line are the deviations and the teal squares are, well, their squared values. The purple square under the plot is the sum of squares: its area is equal to the area of all the teal squares summed together.

Move the line about and change its slope and watch what happens with the teal and purple squares. Have a go!

Which is Which?

Let’s talk about vocabulary for a second. While the term deviation is reserved for differences between data points and their mean, the vertical distances of points from a line of the linear model are called residuals. That’s the term we’re going to be using from now on.

Important

There’s no principled difference between the two, since the mean can be represented as a line in the context of the linear model, but it’s important that you are familiar with the term residual.

So, when we talk about the Sum of Squared Residuals (SSR or SS_R), we mean the total area of these teal squares which is shown in the applet above as the purple square under the plot.

SS_R tells us the amount to which the line (i.e., the linear model) does not fit the data. If the points were all aligned, the line connecting them would have SS_R = 0. This of course, doesn’t happen in real research - we will always have some residual error and if we don’t something has gone wrong.

Finding the Best Line

There are several ways of finding the line of best fit, depending on what your definition of “best” is, but the most straightforward way is to get the line that results in the smallest possible SS_R. This method is called Ordinary Least Squares (OLS) regression because it finds the line with the smallest (least) square.

Play around with with the visualisation and try to find the OLS line of best fit. The line will change colour when you get it right!

Question 7

What is the value of SS_R of the line of best fit in the visualisation? (1 decimal place)

That’s pretty much all there is to it to finding the intercept and slope of the line (there’s a little more maths but we’ll worry about that next year). Of course, we don’t have to find the line of best fit ourselves. We can ask R to do it for us.

Visualisation

Let’s get to work on our analysis today by visualising the relationship between frequency of sexual and romantic attraction on a scatter plot. Here’s the goal:

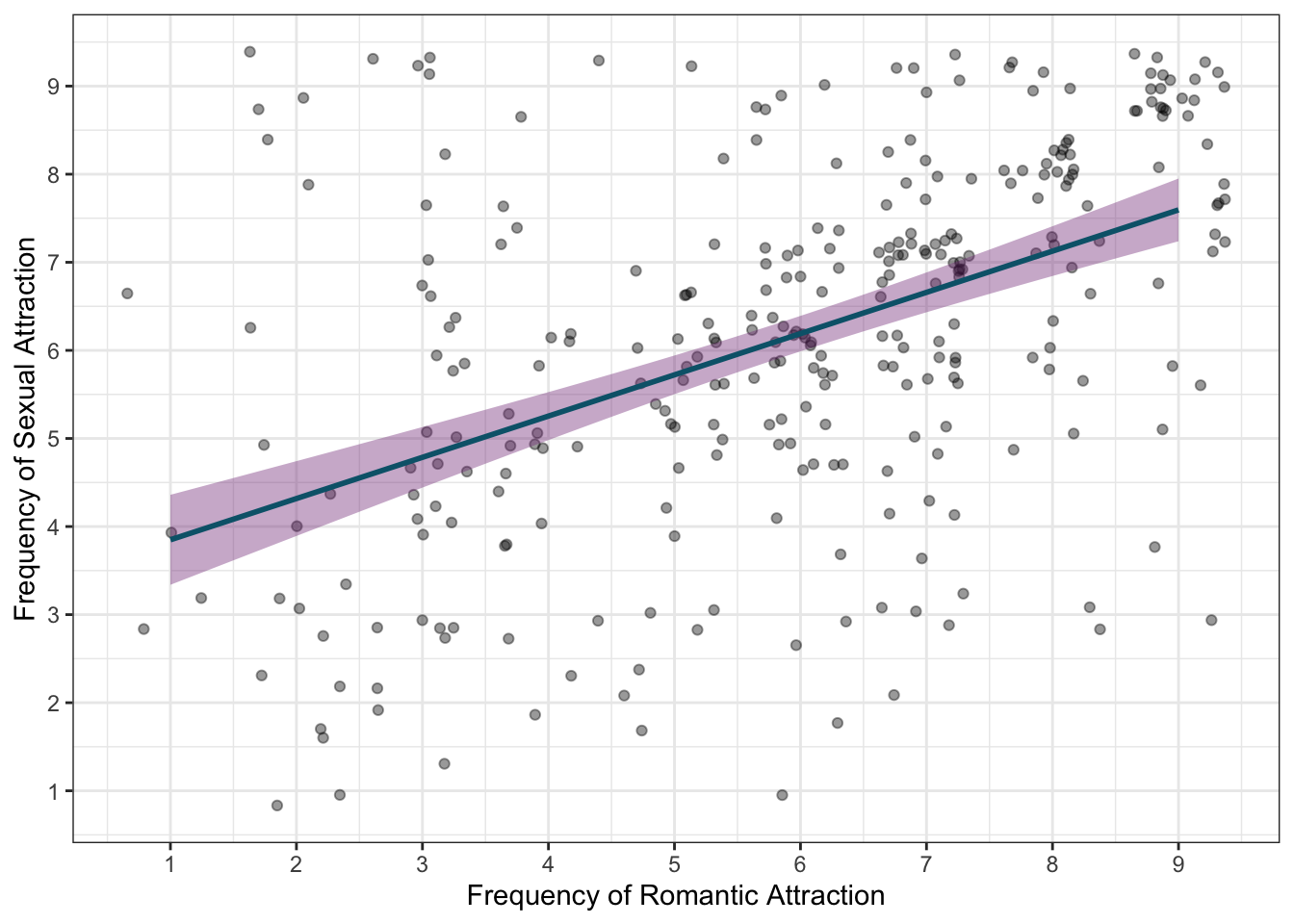
Task 2

Create a scatterplot of frequency of romantic attraction plotted against the frequency of sexual attraction. The basic steps include:

Define a base layer with romantic attraction on the x axis and sexual attraction on the y axis.
Add the “scatter” of points.
Add the line of best fit. You’ll need to set argument method = "lm", for this function, otherwise the line will be wibbly-wobbly.
Adjust labels and set a nicer theme.

Hint

To add a scatter of points, use the geom_point() function.

To add the line of best fit you need the stat_smooth() function. You’ll need to set argument method = "lm", for this function, otherwise the line will be wibbly-wobbly.

Solution

Remember that you can pick any colours for plot, but here are the ones we used:

# create a scatterplot: 
gensex |>  
  ggplot(aes(x = romantic_freq, y = sexual_freq)) +
  geom_point(position = "jitter", alpha = .4) +
  stat_smooth(method = "lm", colour = "#066379", fill = "#833786") + 
  scale_x_continuous(name = "Frequency of Romantic Attraction",
                     breaks = c(0:9)) +
  scale_y_continuous(name = "Frequency of Sexual Attraction",
                     breaks = c(0:9)) +
  theme_bw()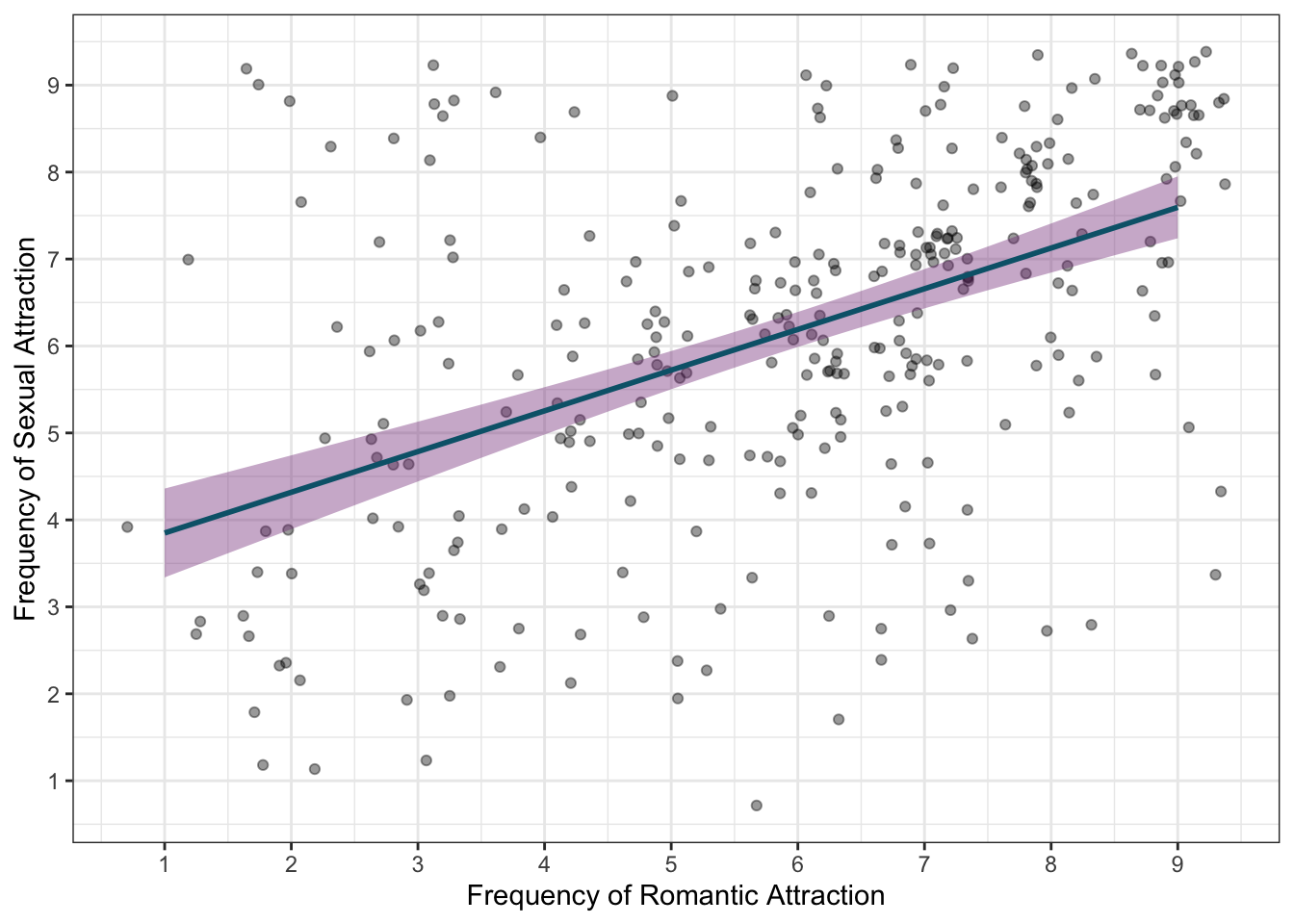

Question 8

What can be said of the relationship between the frequency of romantic and sexual attraction in our sample?

There doesn't seem to be a relationship between the variables As frequency of romantic attraction increases, frequency of sexual attraction tends to decrease The relationship is negative As frequency of romantic attraction increases, so does frequency of sexual attraction

Question 9

Looking at the plot, what do you think is the intercept of this model? Express this as the nearest integer (a whole numebr)

Testing Hypotheses

We’re now ready to fit our model. This time, we’re going to go step further and generate some useful output which we can use to test hypotheses, instead of just learning the value of the intercept and the slope. Let’s fit a model that predicts the frequency of sexual attraction based on the frequency of romantic attraction.

Task 3

Fit the linear model

Fit the model using lm()
Save its output into attract_lm.
Print the result of attract_lm - note down the value of the intercept and the slope.
Extract a summary of this model by piping the model into the summary() function.

Hint

Remember, you need formula and data for the lm() function. Formula takes the form of outcome ~ predictor

Solution

# Fit a linear model: 
attract_lm <- lm(sexual_freq ~ romantic_freq, data = gensex)

# Print the result:
attract_lm


Call:
lm(formula = sexual_freq ~ romantic_freq, data = gensex)

Coefficients:
  (Intercept)  romantic_freq  
       3.3814         0.4682

# Extract the summary
attract_lm |> summary()


Call:
lm(formula = sexual_freq ~ romantic_freq, data = gensex)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.1903 -1.0574  0.2778  1.2142  4.6823 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    3.38137    0.30476  11.095   <2e-16 ***
romantic_freq  0.46816    0.04848   9.657   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.789 on 304 degrees of freedom
Multiple R-squared:  0.2347,    Adjusted R-squared:  0.2322 
F-statistic: 93.25 on 1 and 304 DF,  p-value: < 2.2e-16

As you can see, the summary() function produces quite a lot of output - much more than it appears when you just call the name of the model! So, we can put this model object into other functions to learn more about the model itself.

Let’s break down the summary that R gives us:

Call:
lm(formula = sexual_freq ~ romantic_freq, data = gensex)

This is just R’s way of reminding us what model we are looking at and what function call was used to fit it. We’ll skip the “Residuals” section (that’s for next year, although have a look if you did do the What is “best fit”? section above) and look at the key part of this output:

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    3.38137    0.30476  11.095   <2e-16 ***
romantic_freq  0.46816    0.04848   9.657   <2e-16 ***

This is the most important part of the summary: the model coefficients and their associated statistics. Columns represent different statistics, and there is one row for each of our predictors plus the intercept. We only have one predictor, so we get two rows in total.

Let’s have a look what the columns represent:

Estimate gives the \(b\)-value for each element in the model. At the moment, there’s only one element in the model. The first row is the estimate of the intercept - this is the value of \(b_0\). The second row is the estimate for our predictor romantic_freq - or \(b_1\). Note that these two values are the exact two values that get printed when you just call attract_lm without using any other function.
Std. Error is the estimated standard error of our estimates. Just like we can estimate the standard error of the mean, SEM, we can estimate the standard error of any other estimate. We get one standard error for the intercept and one for the slope. You get the gist.
t value is, well, the t-statistic associated with our estimates and is calculated as the ratio of the first two numbers. For example, the t-statistic for \(b_1\) can be calculated as: \[\begin{aligned}t&=\frac{b_1}{\widehat{SE}_{b_1}}\\&=\frac{0.4682}{0.0485}\\&\approx9.65\end{aligned}\]
Pr(>|t|) is the p-value associated with each t-statistic and, just like any p-value it tells us the probability of getting a t at least as extreme as the one we got if the null hypothesis is true

Important

The null hypothesis with respect to every row of this summary table is that the population value of the parameter (in this case \(b_0\) or \(b_1\)) is zero. If the p-value associated with the test statistic is smaller than our chosen \(\alpha\) level, we reject this null hypothesis and claim that the population value of the given parameter is statistically significantly different from 0.

---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

This is just a legend for the asterisks next to the p-values:

* – result is significant at \(\alpha\) = .05
** – result is significant at \(\alpha\) = .01
*** – result is significant at \(\alpha\) = .001
. – result is significant at \(\alpha\) = .1 (not really used much)

We also have some additional information about the model fit:

Multiple R-squared:  0.2347,    Adjusted R-squared:  0.2322 
F-statistic: 93.25 on 1 and 304 DF,  p-value: < 2.2e-16

As explained in the lecture, R² (here labelled Multiple R-squared) can be interpreted as the proportion of variance in the outcome accounted for by the predictor.

We also have the F statistic. This is the test statistic that tells us whether or not our model is a good fit overall. As for the adjusted R², we will talk about what they are next week.

The F Statistic

The F is yet another signal-to-noise ratio that we can use to test hypotheses. The hypothesis we’re testing with an F statistic is whether adding the predictor (or predictors) into our model results in a sufficient reduction in the sum of squared errors compared the the squared errors in a model with no predictors.

Let’s take this step by step.

Recall the visualisation in the section Finding the Best Line. If we have no predictors in the model, the line in the visualisation will lie flat. In such a scenario, we’re just predicting the outcome from its mean, and the sum of squared errors is calculated as the sum of squared distances of each point from that mean.

Once you start adding predictors, you will typically get a slope (if the predictors are useful). The “squares” on the visualisation now start changing - many of them are shrinking down. So this new sum of squared errors is smaller than the one when the line is just flat without any predictors.

The F statistic is a test of whether this reduction in the sum of squared errors is sufficiently large in order for this model to be of any use. In other words, it asks the question - is this model a good fit? If the p-value associated with the F statistic is statistically significant, we conclude that the model is indeed a good fit and the predictors we’re including are worth the effort.

For the maths curious individuals, here’s the equation (SS_R being sum of squared residuals, df being degrees of freedom), but it’s enough to focus on the conceptual understanding:

\[ F = \frac{SS_{R(\text{no predictors})} - SS_{R(\text{with predictors})}}{df_{\text{no predictors}} - df_{\text{with predictors}}} \div\frac{SS_{R(\text{with predictors})}}{df_{\text{with predictors}}} \]

Question 10

How many coefficients are there in this model? (whole number)

Question 11

What’s the value of the slope? (2 decimal places)

Question 12

Is the relationship between the frequency of romantic and sexual attraction statistically significant at α = .05?

No Yes

Question 13

What proportion of the total variance in sexual attraction is accounted for by romantic attraction? (in % to 2 decimal places)

More detailed summaries

You might have noticed an important element missing from the summary() output above - namely, it didn’t include confidence intervals for b. The summary() of an lm object also doesn’t come in a nice tibble. Luckily, the package broom was written precisely to tidy the output of models into this familiar and convenient format. The package contains a few handy functions we’ll be using quite a bit next year.

Task 4

Use broom functions tidy() and glance() to produce tidy summaries

Take the attract_lm object and pipe it into the tidy() function from broom package to see what it does.
Compare the information here to what you get from summary().
Add the argument conf.int = TRUE to your tidy() command to get confidence intervals for your estimates.
Take the attract_lm object and pipe it into the glance() function from broom package to see what it does.

Hint

Here’s what you’re expected to do:

some_lm_object |> broom::tidy()

Then add the argument for confidence intervals, and do the same for the broom::glance() function

Solution

# get a tidy summary of confidence intervals 
attract_lm |> 
  broom::tidy(conf.int = TRUE)

# A tibble: 2 × 7
  term          estimate std.error statistic  p.value conf.low conf.high
  <chr>            <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)      3.38     0.305      11.1  3.04e-24    2.78      3.98 
2 romantic_freq    0.468    0.0485      9.66 2.04e-19    0.373     0.564

# get a tidy summary of model fit statistics: 
attract_lm |> 
  broom::glance()

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.235         0.232  1.79      93.3 2.04e-19     1  -611. 1228. 1240.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

The last two columns of the table produced by the tidy() function give us the lower and upper confidence intervals. The first row is for the intercept, and the second one is for the effect of our predictor. Remember that confidence intervals tell us the plausible value the parameter can take in the population, assuming our sample is one of the 95% that indeed contain the true population value. Under this assumption, the population value for the effect of romantic_freq can be as low as 0.37, or as high as 0.56.

The output of the glance() function, provided you gave it a lm object, will only ever have one row with all the various model fit statistics. We will talk about some of these in the coming months but for now, the most important is the r.squared column containing, you guessed it, R², and the statistic column, which contains the F statistic.

Unhelpfully, both broom outputs label their statistics as statistic. So if you’re ever unsure which one is t and which one is F, you can use the summary() to remind yourself

Reporting Results

Now that we have the results from our linear model, we can report them. Let’s look first at reporting the results in text, then making them into a nice table.

In-Text Reporting

In-Text Example

The model was overall a good fit, \(F(1, 304) = 93.25\), \(p < .001\) and accounted for a substantial proportion of variance in the frequency of sexual attraction, \(R^2 = .23\). Frequency of romantic attraction was positively related to sexual attraction, with sexual attraction increasing by 0.47 rating point for each point increase of romantic attraction, 95% CI [0.37, 0.56], \(t(304) = 9.66\), \(p < .001\).

Let’s look at each bit of this paragraph step by step.

First, we report the overall model fit with the F statistic, degrees of freedom, and the associated p-value. Then we report R², as a decimal (rather than a percentage), to give an idea about the amount of variance explained.

Once we’ve reported the overall model fit, we should report the relationship of interest and, once again, provide evidence by quoting the relevant coefficient and its statistical test. In our case, we’re only interested in the slope (\(b_1\)) because it is the slope of the line that tells us about the relationship between our predictor and outcome. To fully report the relationship, we need the following information, which we can find in the output from either summary() or broom::tidy().

The value of the relevant \(b\) coefficient with a 95% CI
The t-statistic of the test of statistical significance of the coefficient: its name (t), the correct number of degrees of freedom, and its value. The degrees of freedom for the t statistic are the same as for the overall F statistic.
The p-value associated with the test

It is nice to tell the reader what this relationship looks like by telling them what change in the outcome is associated with a unit change in the predictor.

Table Reporting

It’s most useful to report your results in a table when you have multiple predictors, or more complex models that would be repetitive or confusing to explain in text. However, we can make a beautiful model table fairly quickly, so let’s have a go now! When we’re done, it’ll look like this:

Term	b	SE	t	p	95% CI
(Intercept)	3.38	0.30	11.10	< .001	[2.78, 3.98]
romantic_freq	0.47	0.05	9.66	< .001	[0.37, 0.56]

Task 5

Create nice tables to report the results of your model

Start with the output from tidy()(including confidence intervals) and pipe into the nice_table() function from the rempsyc package.
We need to tell nice_table what kind of broom object we’re using. We created our model using the lm() function, so we can set the argument broom = "lm" inside of nice_table().

Hint

You can re-use the broom::tidy() code from the previous exercise. Then you need to add one more line to it.

Solution

# create a nicely formatted table using rempsyc
report_model |> 
  broom::tidy(conf.int = TRUE) |> 
  rempsyc::nice_table(broom = "lm")

Term	b	SE	t	p	95% CI
(Intercept)	3.38	0.30	11.10	< .001	[2.78, 3.98]
romantic_freq	0.47	0.05	9.66	< .001	[0.37, 0.56]

That’s all for this week - nice work!

ChallengR

ChallengR Time!

This task is a ChallengR, which are always optional, and will never be assessed - they’re only there to inspire you to try new things! If you solve this task successfully, you can earn a bonus 2500 Kahoot Points. You can use those points to earn bragging rights and, more importantly, shiny stickers. (See the Games and Awards page on Canvas.)

There are no solutions in this document for this ChallengR task. If you get stuck, ask us for help in your practicals or at the Help Desk, and we’ll be happy to point you in the right direction.

Task 6

The Higher Wizardry Education Academy (HWEA) has conducted a study investigating whether students’ ancient rune-coding skills can be predicted by their perseverance. The study ran across different wizarding institutes.

The data is stored in the sorcery_df dataset, which you can read in using the code-chunk below. The Grand Matrix Master has already analysed the data and written up the conclusion, which you can also read in the code-chunk below. Explore the results object to see what The Grand Matrix Master has learnt.

sorcery_df <- here::here("data/sorcery_df.csv") |> readr::read_csv()

results <- here::here("data/results.rds") |> readRDS()

Unfortunately, The Grand Matrix Master has been unkind to his research apprentice. The apprentice has placed a curse upon The Master’s results file and corrupted the report before vanishing in a puff of rainbow glitter and confetti. The report is now unreadable!

“You there!” The Matrix Master barks in your general direction. “You, with your funny computing machine! Fix this now, or so help me Dog, you’ll be calculating covariances by hand for the next year!” He slams the door as he storms out, leaving you in the rainbow-covered apprentice office.

You try to run the report through the “UncorruptoR” - a device you invented that can help recover information from cursed report files:

secret_key <- "XXXXXX"

results |> 
  safer::decrypt_string(key = secret_key)

Alas! The “UncorruptoR” will only work with the right key. Without it, there is no chance of recovering the report.

As you stand there contemplating your career choices, a larger piece of confetti on the floor catches your eye. You pick it up, and notice there is a message written on it. The message says:

The answer to your woes is scattered in the model for the school that explains the most of variance.

What could it mean? Use the secret message and the sorcery_df dataset to work it out!

…

That’s quite right, you think to yourself after finishing the task. You know what you need to do next.

Footnotes

Pronounced as “why aye” or “why sub-aye”.↩︎